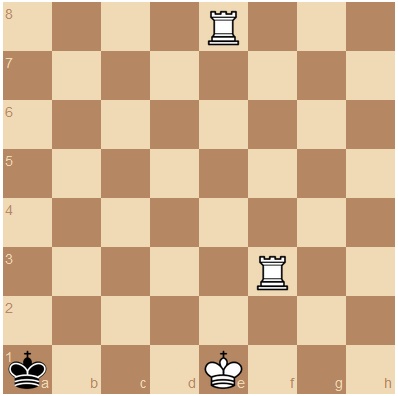
Posición
Blancas: Re1; Te8; Tf3
Negras: Ra1
Juegan blancas y dan mate en 2.
El día ideal para poner este problema es sin duda el 28 de Diciembre o en su defecto, jornadas especiales como la última clase del año o fin de curso.
La solución, pilla donde las haya, no deja de ser instructiva tomando en consideración la siguiente explicación:
Hasta finales del siglo XX, la normativa FIDE decía:
«El enroque es una jugada con el rey y una torre. El rey se mueve en línea recta a la siguiente casilla del mismo color, reduciendo la distancia entre él y la torre que participa en el enroque. Entonces la torre se mueve sobre el rey para ocupar la casilla que el rey acaba de cruzar. El enroque no puede tener lugar si el rey o la torre ya se han movido. El enroque se previene temporalmente si: a) hay cualquier pieza de cualquier color entre la torre y el rey; b) si la casilla en la que el rey está, o la que tiene que cruzar, o la que va a ocupar, está bajo ataque de una o más piezas del oponente. Estas condiciones no se aplican a la torre».
Pero Max Pam, ideó el problema planteado cuya solución respeta escrupulosamente dicha normativa. Para hallar la solución es preciso tomar en consideración de dónde proviene la torre sita en e8.
Esta travesura, forzó a la FIDE a modificar su normativa sobre el enroque, especificando que debía acontecer en la primera u octava fila.